目录
快速导航-
卷首语 | 做好数学教育加法 助力创新人才培养
卷首语 | 做好数学教育加法 助力创新人才培养
-

教材点击 | 通过“数与代数”领域发展学生推理能力的三条途径与教学建议
教材点击 | 通过“数与代数”领域发展学生推理能力的三条途径与教学建议
-

教材点击 | 凸显数系扩充过程 强化核心素养导向
教材点击 | 凸显数系扩充过程 强化核心素养导向
-

教学研究 | 以问题设计为载体满足学生的思维需求
教学研究 | 以问题设计为载体满足学生的思维需求
-
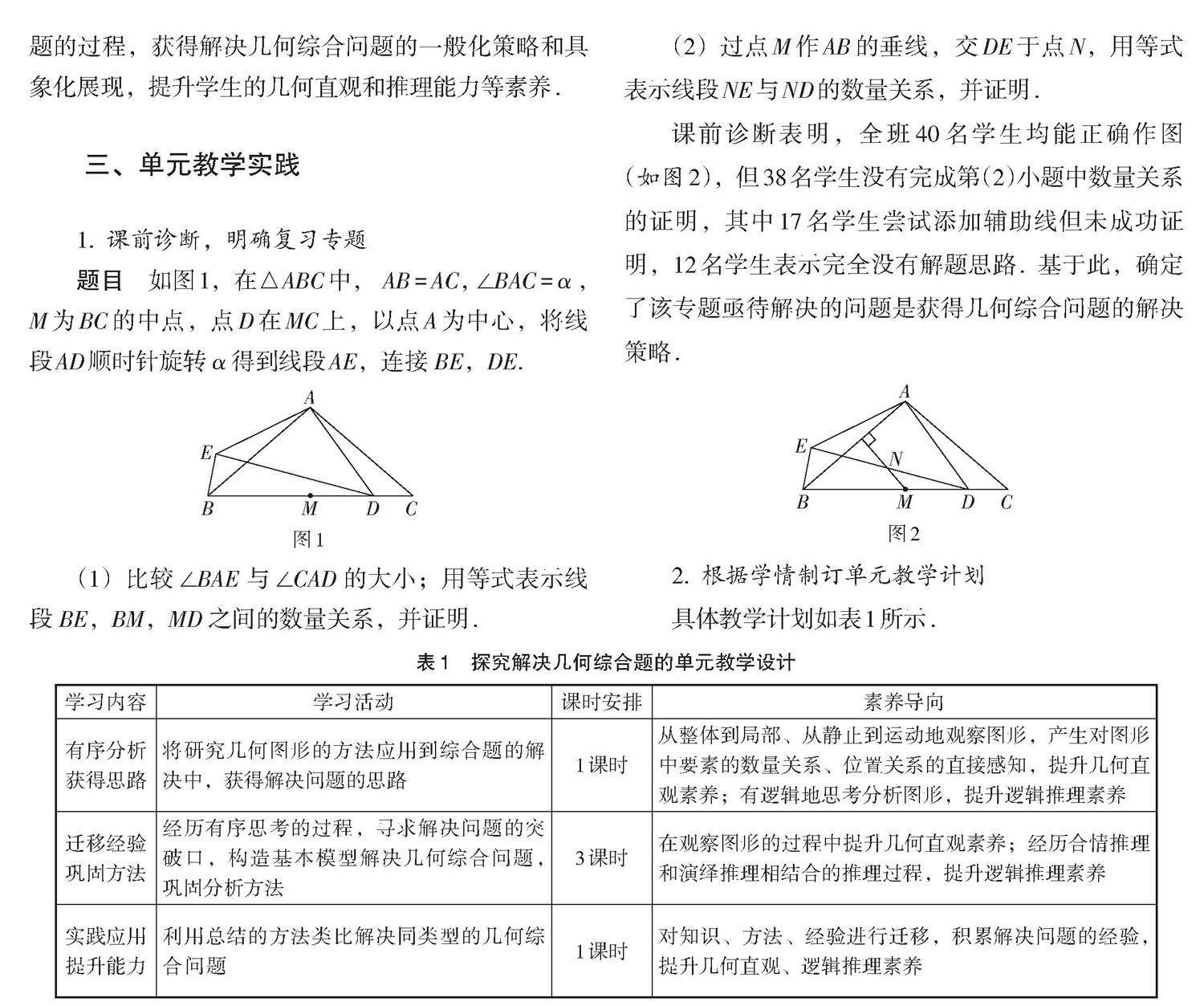
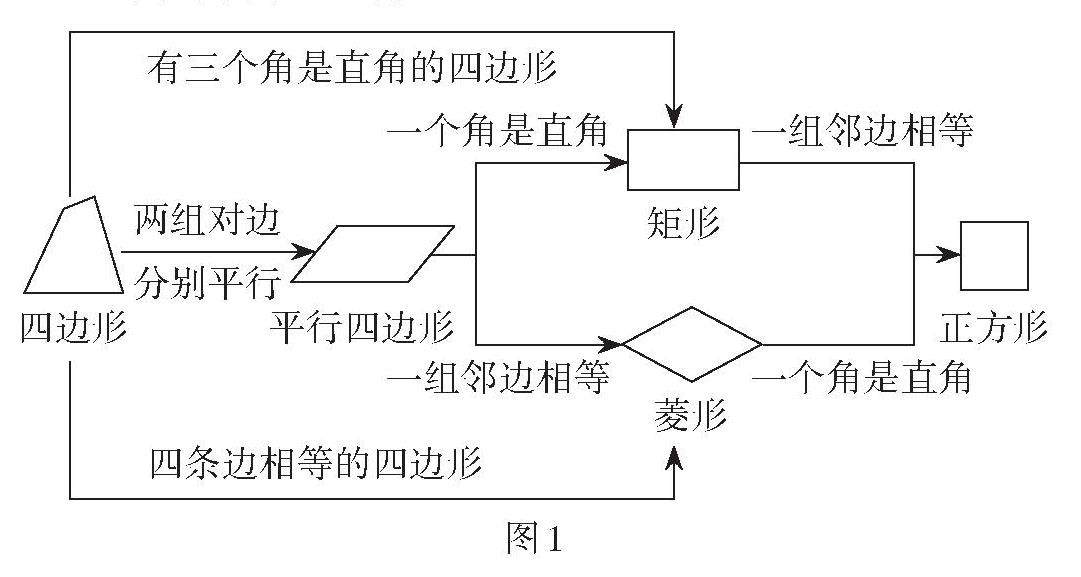
教学研究 | 基于核心素养的中考图形与几何复习课的教学实施策略
教学研究 | 基于核心素养的中考图形与几何复习课的教学实施策略
-
教学研究 | 对话意识:基于深度学习的课堂教学应然要求
教学研究 | 对话意识:基于深度学习的课堂教学应然要求
-

教学研究 | 发展初中生抽象能力的教学实践
教学研究 | 发展初中生抽象能力的教学实践
-

教学研究 | 育人视域下试卷讲评课的教学改进
教学研究 | 育人视域下试卷讲评课的教学改进
-
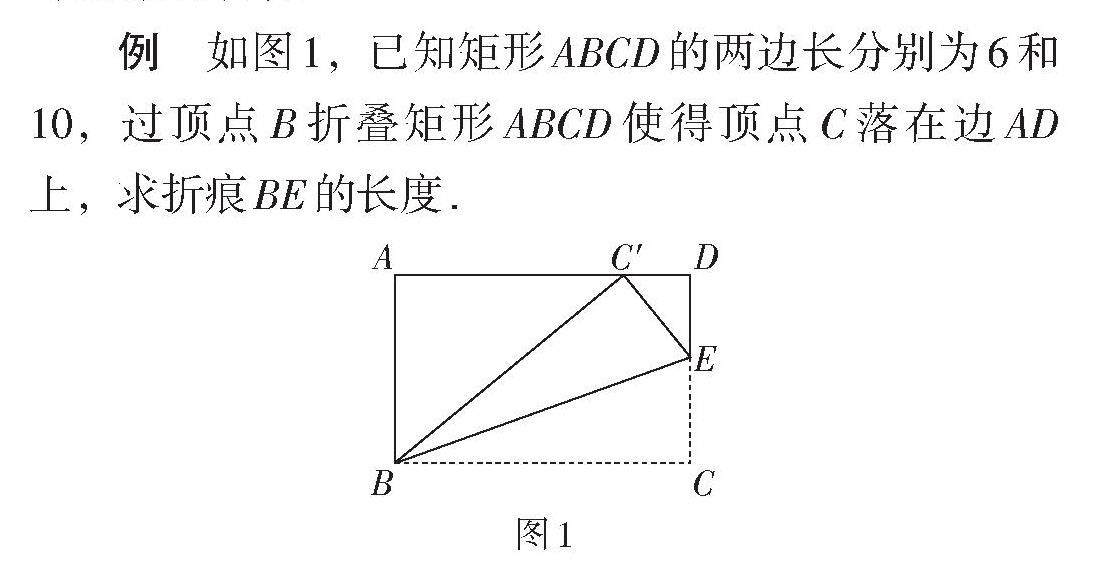
实践探索 | 折纸——折叠类问题教与学的“脚手架”
实践探索 | 折纸——折叠类问题教与学的“脚手架”
-
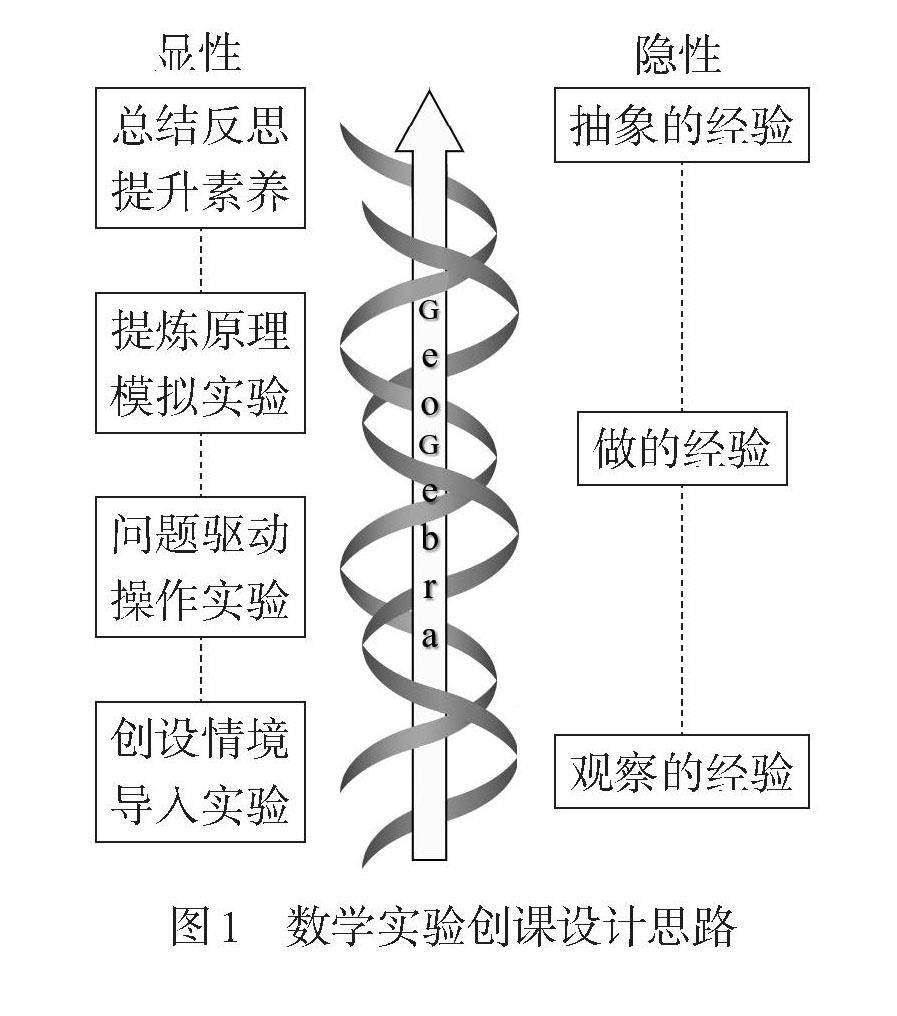
实践探索 | 基于可视化实验探究的初中数学创课设计
实践探索 | 基于可视化实验探究的初中数学创课设计
-

案例透视 | 初中数学单元学习任务整体设计的思考与实践
案例透视 | 初中数学单元学习任务整体设计的思考与实践
-

案例透视 | 基于CPFS结构解题教学的案例分析与思考
案例透视 | 基于CPFS结构解题教学的案例分析与思考
-
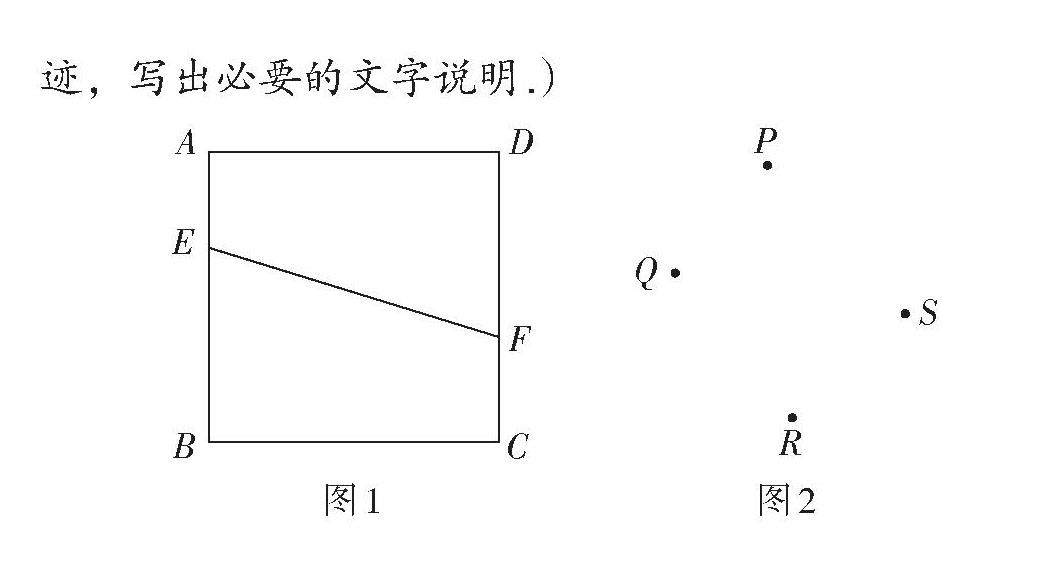
试题研究 | 尺规作特殊图形的构图思路探析
试题研究 | 尺规作特殊图形的构图思路探析
-

他山之石 | 学段视角下中法义务教育知识与数学核心素养的比较研究
他山之石 | 学段视角下中法义务教育知识与数学核心素养的比较研究















 登录
登录